
W = ?
AB AC
M = 100 Mpa = 100X106 M = 50 Mpa
A = 400 mm2 = 400X10-6 A = 200 mm2
P = 40 Kn P = 10Kn
Py = (sen 30) (40) Py = 7,071.06
= 30,000
Px = (cos 30) (40) Px = 7,071.06
= 34,641.01
Σ Fy = Q Σ Fx = R
TBA + TAC – W TBA + TAC – W
(40 sen 30) + (10 sen 45) – W = 0 - (40 cos 30) + (10 cos 45) = R
20 BA + 7.07 AC = W - 34.64 TAB + 7.07 TAC = 0
20 AB + 70.7 (4.89 TAB) = W TAC = = 4.89 TAB
TAB = (400X10-6) (100X106) - 775 W =A6
W= 2182.8 X103 N
W = 12893.44
Σ Fx = TAC cos 45 – TAB cos 30 = 0
Σ Fy = TAC sen 45 + TAB sec 45 – W = 0
TAC = = 1.22 TAB = -775W
1.22 TAB sen 45 + TAB sen 45 = W = A6
.866 TAB + .707 TAB = W
TAB = W
W = (100X10 6) (400)
Determine, para la armadura de la figura, las áreas transversales de las barras BE, BF, CF, de modo que los esfuerzos no excedan de 100 MN/m2 en tensión ni de 80 MN/m2 en compresión. Para evitar el peligro de un pandeo, se especifica una tensión reducida en la compresión.
A = ?
T = 100 MN/m2 100,000 (tensión)
T = 80 MN/m2
2 MB = 0
- (3 m) (40,000) – (6 m) (50,000) – (8 m) (CF) = 0
CF = 52,500 N (compresión)
2 MF = 0
- (3 m) (50,000) – (4 m) (EB cos 53.13)
EB = 62,499.85 N (tensión)
Σ Fx= 0
CF – EBX – BFX = 0
52,500 – 37,500 = (BF x cos 69.44)
BF = 42,712.11 N (tensión)
CF = A = = = 6.56 X 10-4 = 6.56 cm2
EB = A = = 6.25 cm2
BF = A = = 4.27 cm2
Una barra homogénea AB (de 150 kg) soporta una fuerza de 2-kN. La barra está sostenida por un perno (en B) y un cable (CD) de 10mm de diámetro. Determine el esfuerzo ejercido en el cable.
T cable =
ΣMb = (T X F)b = 0
(6 m) (2000) + (3 m) (1470) – (3 m) (T sen 53.13º)
T = 6,837.5 N
T cable = = 87,102,027.53 Pa = 87.102 Mpa
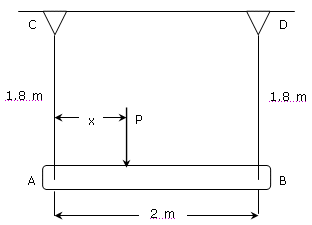
Una barra homogénea AB (de 1000 kg de masa) pende de dos cables AC y BD, cada uno de los cuales tiene un área transversal de 400 mm2, como se observa en la figura. Determine la magnitud P, así como la ubicación de la fuerza adicional máxima que se puede aplicar a la barra. Los esfuerzos en los cables AC y BD tienen un límite de 100 MPa y 50 MPa, respectivamente.
PAC = (100x106) = 40,000 N
P = TA
PBC = (50X106) (400X10-6) = 20,000 N
Σ Fy = 0
40,000 + 20,000 – 4800 – P = 0
P = 50,200 N
Σ MA = 0 (r x f)
- (1 m) (9800 N) + (2 m) (20,000) – (x) (50,200) = 0
X = 0.601 m
Un recipiente cilíndrico a presión está fabricado de placas de hacer que tienen un espesor de 20 mm. El diámetro del recipiente es 500 mm y su longitud, 3 m. determine la máxima presión interna que puede aplicarse si el esfuerzo en el acero esta limitado a 140 MPa. Si se aumenta la presión interna hasta que el recipiente fallara, bosqueje el tipo de fractura que ocurrirá.
TAC = 140 Mpa
A = 3.61X10-4 m2
- ΣAC = 200 G Pa
- L = 3 m
ΣAC = 7X10-9 m/m
T = 2.1X10-3 m
P = 11.2 MPa
Calcula el mínimo espesor de la placa que forma el deposito si el esta admisible es de 40 MN/m2 y la presión interior vale 1.5 MN/m2.
T = 40 Mn/m2 = 40X106 Pa
P = 1.5 MN/m2 = 1.5X106 Pa
Esp = ?
d = 600X10-3 mm
t = 0.01125 m
Una barra de aluminio de sección constante de 160 mm2 soporta unas fuerzas axiales aplicadas. Si E = 70 GPa, determina el alargamiento o acortamiento total de la barra. (No hay pandeo).
A = 160 mm2
Σ = 70 Gpa
T = ?
Si =
AE = (160x10-6) (70X109) = 11.2X106
& = = -5.35X10-4 m
& = = 1.78 X 10-3
& = = 6.25X10-3
& = 7.5X10-3 m = 7.5 mm
Un tubo de bronce de 150 mm de longitud, cerrado en sus extremos, tiene 80 mm de diámetro y 3 mm de espesor. Se introduce sin holgura en un bloque absolutamente rígido e indeformable y se somete a una presión interior de 4 Mn/m2/m2. Con los valores v = 1/3 y E = P3x103 MN/m2. Determinar el esfuerzo circunferencial del tubo.
P = 4 Mn/m2
V = 1/3
E = 83X103 MN/m2
T = ?
A = ¼ p (74X10-6)
A = 5.81X10-5 m2
& = = = 0.124 m
E = = = 0.829 m/m
T = EG = (83X103 MN/m) (0.829 m/m)
T = 68.846.81
Un tubo de aluminio de 200 mm de largo, cerrada en sus extremos, tiene 100 mm de diámetro y una pared de 2 mm de espesor. Si el tubo cabe justamente entre dos paredes rígidas con presión interna nula, determine los esfuerzos longitudinal y tangencial para una presión interna de 4.00 MN/m2. Suponga v = 1/3 y E = 70 x 104 N/m2.
L = 200X10-3
D = 100X10-3
T = 2X10-3
P = 400 Mpa
E = 70X09 Pa
Tl =100 MPa
Tc = 50 MPa







No hay comentarios:
Publicar un comentario